ゼロイチです！
今回は私たちが日常で使っている10進数を他の進数に変換する方法を見ていきましょう！
整数部の変換
まずは整数の変換です。
整数の10進数を2進数や8進数、16進数に変換するには、
変換したい10進数を商が0になるまで求めたい基数（※）で割り続け、その商と余りを求めればいいんです。
これで求めた余りの部分が変換結果になります！？
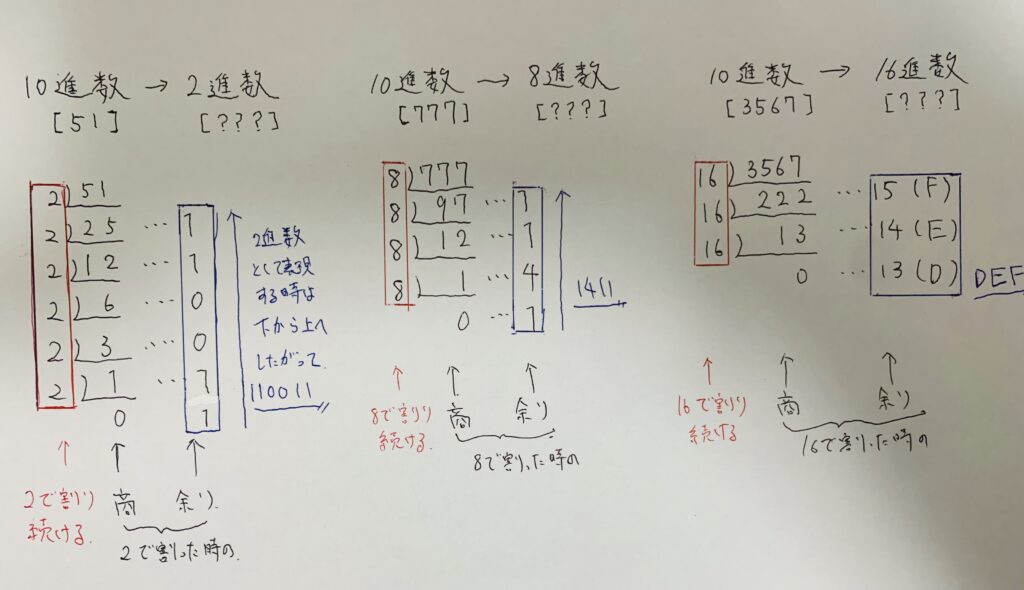例えば上の画像で、10進数を2進数にしたいときは2で割り続けます。
51を2で割ると商は25、余は1ですね。
筆算では普通商は整数の上に、余は下に書いていたと思いますが、やり方は似ていますね！
これを続けていきと青枠に余りだけの列ができます。枠内の数値を下から並べた数値が2進数への変換結果になります！
8進数、16進数も同様でなぜその基数で割るのかというと余りが基数以上にはならないからですね！
ポイント
10進数の整数をn進数へ変換したい時は、
①変換したい10進数を商が0になるまでnで割り続け商と余りを求める（下方向に計算）
②縦に並んだ余りを下から並べる
小数部の変換
次に小数の変換です。
小数の10進数を2進数や8進数、16進数に変換するには、
変換したい10進数の小数部を小数が0になるまで基数でかけ続ける。
これで求めた整数部分が変換結果になります！
例えば上の画像で、10進数の小数を8進数にしたいときは8をかけ続けます。
0.9140625に8をかけると7.3125ですね。
そして小数部分の0.3125に再度8をかけます。
すると2.5で、小数部分0.5にまた8をかけると4.0となり、小数部分が0になりました！
ここで計算終了です。
青枠は計算過程で無視した整数部分になります。枠内の数値を上から並べた数値が8進数への変換結果になります！
2進数、16進数も同様です！
ポイント
10進数の小数をn進数へ変換したい時は、
①変換したい10進数の小数を小数部分が0になるまでnでかけ続ける。（下方向に計算）
②縦に並んだ整数部分を上から並べる
無限小数（循環小数）
今回取り上げた10進数の小数はどれもn倍し続けた時に小数部が0になり、このようなケースは「有限小数」と呼ばれます。
数値によっては、小数部が0にならない場合があります。
例えば10進数の0.4を8進数に変換すると0.31463146となり3146が繰り返され整数部がゼロになりません。
このような小数を『無限小数』といい、さらに同じ数値が繰り返される場合を『循環小数』といいます。
無限小数の場合、コンピューターは数値の近似値で数値を表します。