どうもゼロイチです!
突然ですが、コンピュータが数を表すやり方は2つあります!
コンピュータの中での数と約束事
一つ目は、「固定小数点数」と呼ばれ、
小数点(、)の位置をあらかじめ決められた数になります。
もう一つが、「浮動小数点数」というもので、
小数点の位置が可変の数になります。
そして覚えるべきは二つあります。
ポイント
コンピュータの中では、
整数は、固定小数点数で表す
実数(小数も含む)は、浮動小数点数で表す
固定小数点数
上記の通り、
「固定小数点数」について、頭4bitを整数とすると数字が8桁のbit列の場合、「〇〇〇〇.△△△△」の○が整数部分、△が小数部分になります。
なので最下位bitの右側を小数点にすると決めてしまえば小数部分はなく、整数だけを扱えるようになりますね!(「〇〇〇〇〇〇〇〇.」のよう)
8bitの固定小数点数で表される整数の範囲は次のようになります。
符号ビットあり
| 2進数 | 10進数 | |
| 最小 | 00000000 | 0 |
| 00000001 | 1 | |
| ↓ | ↓ | |
| 11111110 | 254 | |
| 最大 | 1111111 | 255 |
n bitで表現できる範囲は、
0〜2n-1
(8bitなら28-1=256)
符号ビットなし
| 2進数 | 10進数 | |
| 最小 | 10000000 | -128 |
| ↓ | ↓ | |
| 0 | 00000000 | 0 |
| ↓ | ↓ | |
| 最大 | 01111111 | +127 |
n bitで表現できる範囲は、
-2(n+1)~2(n-1)-1
(8bitなら-29~29-1=-128~127)
浮動小数点数
浮動小数点数は指数表記を用いて数値を扱います。
例えば、以下のようです。
0.000003 → ± 0.3 × 10-5
ポイント
一般化すると浮動小数点数は以下のようです。
± m × 2e
(m:仮数、2の部分:基数、e:指数)
このようにすると、以下のようになるので大きな値も小さな値もこの形で表されます。
ついでに32bitので表した浮動小数点数も紹介します。
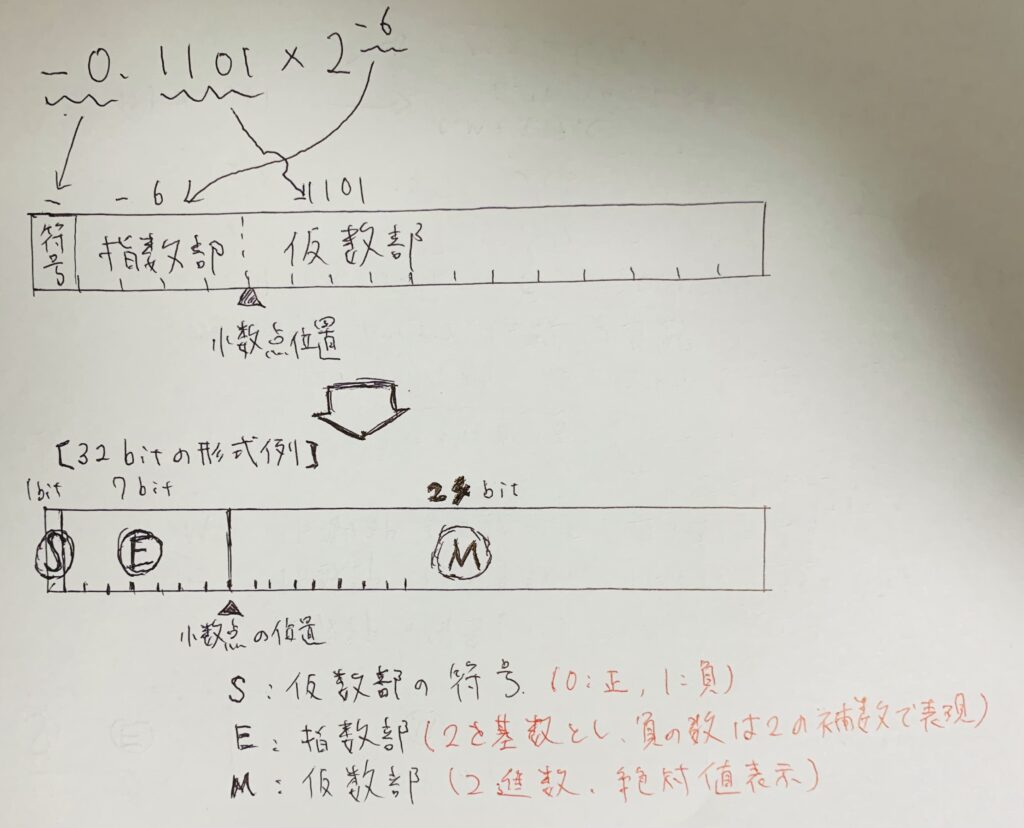
例えば、
10進数「 0.4375」を一般的な32bit形式にする。
①2進数にし、0.Mの形に正規化する。
0.0111 → 0.111 × 2-1
②S、E、Mを求める
S(符号) → 0
E(指数部)→ 1111111(10進数「-1」を2進数の2の補数で表す)
M(仮数部)→ 111
③32bitに当てはめると、
0|1111111|111000000000000000000
-

-
10進数から2進数、8進数、16進数へ!
ゼロイチです! 今回は私たちが日常で使っている10進数を他の進数に変換する方法を見ていきましょう! 整数部の変換 まずは ...
続きを見る
-

-
2進数の足し算・引き算(補数)
ゼロイチです! これまで進数について概念を説明してきましたが、今回は勉強した知識を活用してみましょう! そう、四則演算に ...
続きを見る
正規化
もう一つ大事なのが正規化ですが、
これは小数点の位置を調整することで、有効な桁数が多く取れるようになります。
例えば、0.001234 × 10-5 なら 0.1234 × 2-7
0.00000101 × 10-5 なら 0.101 × 2-10
というように小数点の隣に数字がきます!
IEEE754での浮動小数点数
IEEE(米国電子電気技術者協会)により規格化されたのがIEEE754になります。
32bit、64bit、128bitの型式があります。
今回は、前項に合わせて、32bitを見ていきます。

ポイント
IEEE754形式では一般的な32bit形式と違い、
Eの指数部はバイアスにのせて正の数で表す
Mの仮数部は「1.M」とすることで、「0.M」と表すよりも少ないbit数で表せる
例えば、
10進数「 0.4375」をIEEE754形式にする。
①2進数にし、1.Mの形に正規化する。
0.0111 → 1.11 × 2-2
2bit左にシフトするので「0.M」より指数部分は(-1)増える。
②S、E、Mを求める
S(符号) → 0
E(指数部)→ 01111101(バイアス表現なので-2+127=125でこの2進数)
M(仮数部)→ 11
③32bitに当てはめると、
0|01111101|11000000000000000000
理解できましたでしょうか。そうであれば嬉しいです!