どうもゼロイチです!
今日勉強していくのは、「シフト演算」です!
これは2進数を表すビット列を、左もしくは右にずらす操作のことを言います。
結論から言うと、
ビットの並びを左にずらしたり右にずらしたりすると、
元の値の2倍や1/2倍という計算が簡単にできるんです!
ポイント
・シフト演算は、2進数を表すビット列を左や右にずらす操作のこと
・ビット列を左や右にずらすと、元の値の2倍や1/2倍になる
・シフト演算には①論理シフトと、②算術シフトがある。
①論理シフト:符号を考慮せずにシフト演算を行うこと
②算術シフト:符号を考慮してシフト演算を行うこと
論理シフト
前項で説明したように、論理シフトは符号を考慮しません。
つまり、最上位のビットも含めて何も考えずにシフトすることです。
そしていくつシフトさせるか、つまりシフトするbit数に応じて何倍になるか変わってきます!
先にまとめておくと、
ポイント
"n"bit分の
左方向への論理シフトでは、元の値の"2n"倍になる
右方向への論理シフトでは、元の値の"1/2n"倍になる
例は以下のようです。
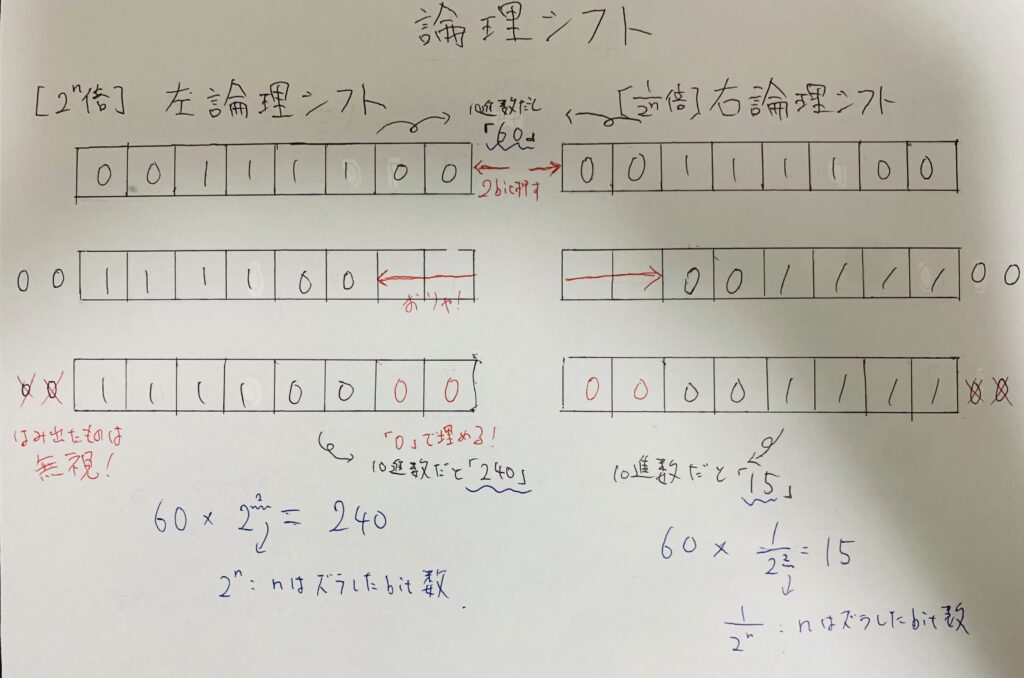
注意ポイント
左論理シフトで、はみ出した数字が"1"の場合、前提のbitで表される範囲を越え変な数字になります。
これを「オーバーフロー」と言う。
右論理シフトで、はみ出した数字が"1"の場合、はみ出した数字は割り算した結果の余りなので、0で割り切れない数字を意味しています。
算術シフト
算術シフトでは、先頭の符号ビットを固定します。それ以降のビットだけを左右にシフトします。
ポイント
先頭の符号bitは固定した状態で "n" bit分、
左方向への算術シフトでは、元の値の"2n"倍になる
右方向への算術シフトでは、元の値の"1/2n"倍になる
例は以下のようです。
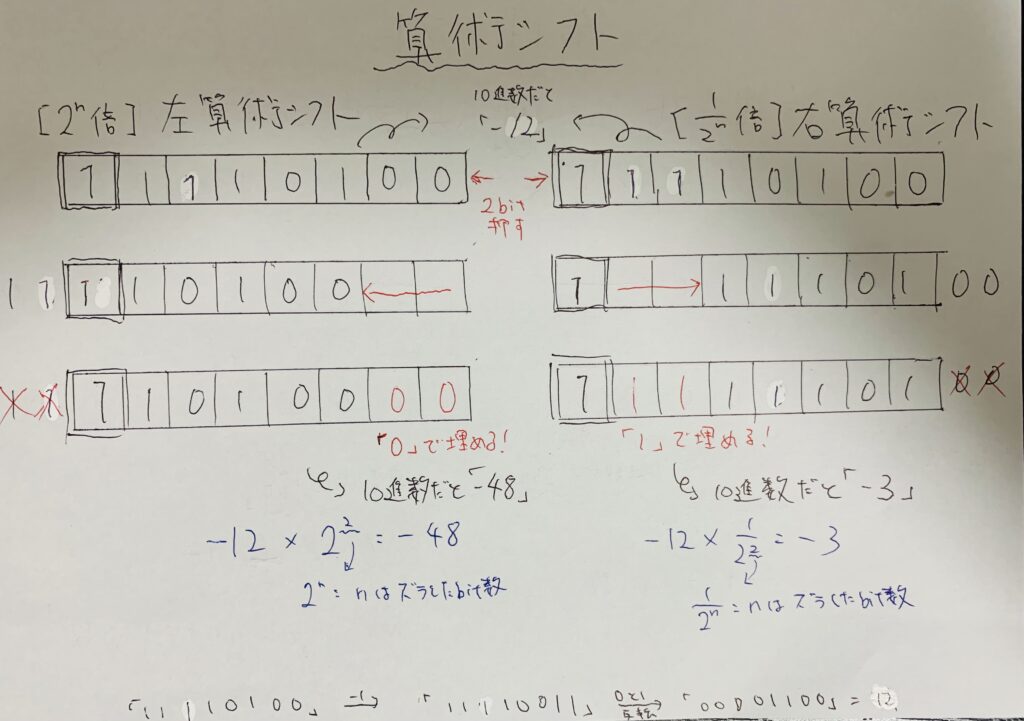
注意ポイント
左論理シフトで、符号ビットと異なる数字がはみ出した場合は、変な数字になるので「オーバーフロー」となる
右論理シフトではズラした後の空欄は、符号ビットと同じ数字で埋める
次回はこれらを使って掛け算と割り算を見ていきます!